Featured

Moving from Mimicry to Meaningful Learning

Ever been in a classroom that feels more like a sleep-inducing seminar? I can see you raising your hand. You know the scene: students zoning out, fidgeting like they’re auditioning for a tap dance, begging for bathroom breaks like they’re fleeing a sinking ship. As both a former student and now a teacher, I’ve danced this engagement tango more times than I care to count.

But here’s the kicker that’s evident this year: engagement isn’t a one-size-fits-all deal, especially in the wild world of math classrooms. Elementary? It’s about those manipulatives and building conceptual understanding. Middle school? Cue the shorter classes and the panicked rush to cover everything before the state tests roll in. And as for high school? Well, that’s a beast I’ve yet to wrestle with, but who knows, it might be in my cards someday.

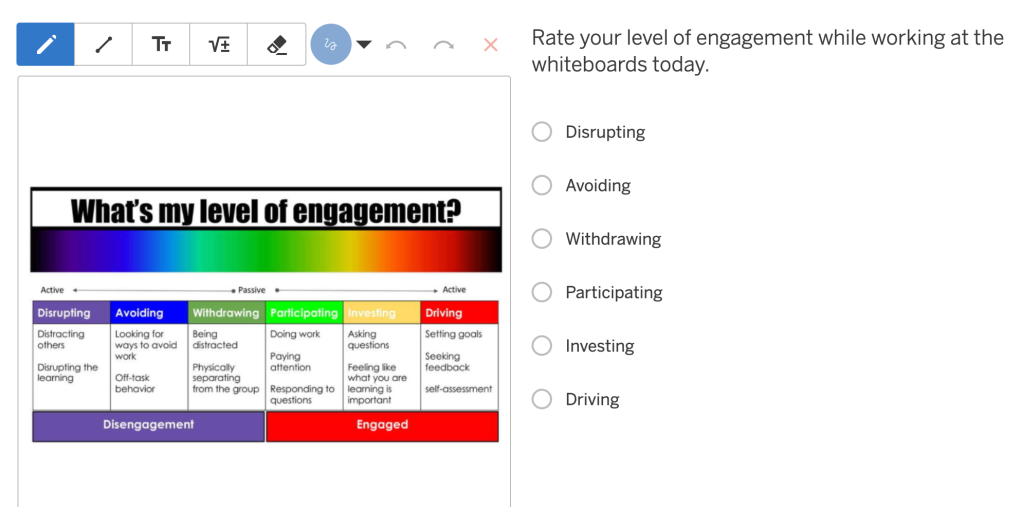
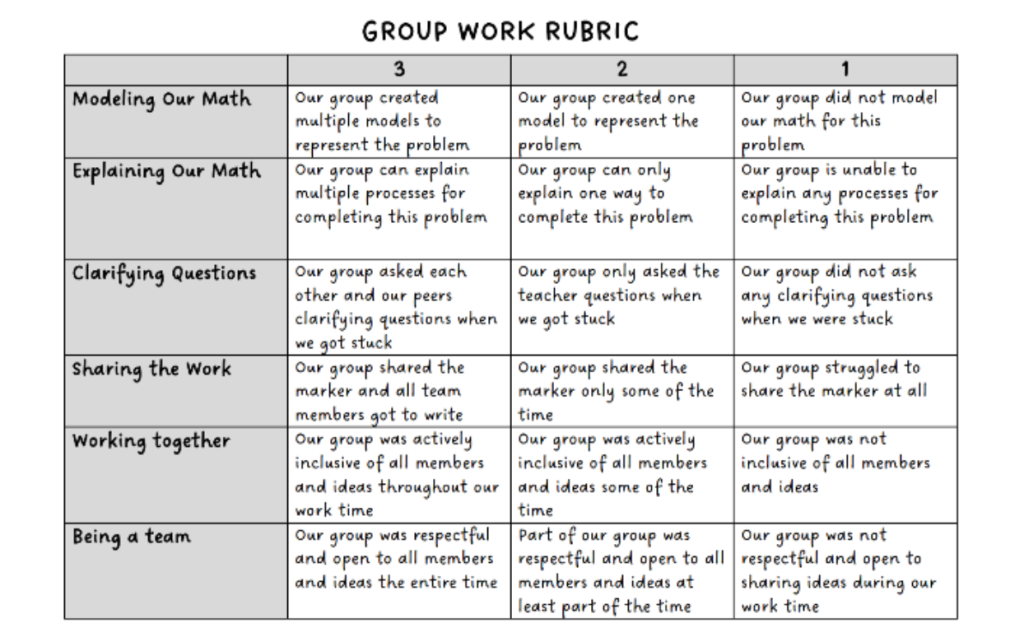
Enter the game-changer: whiteboards and math chitchat, courtesy of Peter and his Building Thinking Classroom book. Since August, my 6th grade team and I have been riding this engagement wave. And you know what? It’s working. Students are gabbing, reasoning, and proudly displaying their work like they’re auctioning off masterpieces. Math class has become more of a lively arena of self-advocacy and problem-solving prowess.

Sure, it’s not all rainbows. We’ve had our fair share of hits and misses. We’re a math team, wielding OUR, Desmos, and BTC as our trusty resources. Some tasks hit the mark, turning mundane math into whiteboard wizardry. Others? Well, let’s just say we’ve had a few duds.

But here’s the rub: engagement doesn’t always translate to learning. Case in point: my recent tests were a wake-up call. The kids were jazzed (as jazzed as they can be about multiplying decimals), but did they really grasp the concepts? I remember many lessons as a kid that I thought were amazing, but I have no ideas what was learned in the process. That’s where the consolidation struggle begins and hasn’t quite ended. Picture this: students work in whiteboard groups, snap a pic of their whiteboards, we chat briefly as a class, and then… crickets. I’ve got a handful of students keeping the convo alive, but the rest? MIA.

So, what’s the plan? I’m brewing up some ideas: group summaries, solo reflections, you name it. And those “notes to my future forgetful self” that I’ve been using? They’re due for a makeover—less procedural, less mimicky and more self-advocacy pep talk.

But hey, despite the hiccups, BTC has bene great this year. I’ve even put in a request for more whiteboards next year. Here’s to another year of math magic, with a few tweaks along the way.

First Education Math Summit with Peter Liljedahl

This past Thursday I attended the First Education Math Summit.  Peter Liljedahl was the keynote speaker and this post is designed to synthesize what I heard and take positive steps moving forward as I continue to implement BTC strategies in the classroom. As a middle school math teacher, I’ve embarked on a journey this school year to enhance critical thinking among my students. The insights I’ve gained from implementing Breakout (BTC) strategies have been interest to reflect on and I feel like have helped my practice. Takeways from the keynote are below.

The Link Between Thinking and Learning

Peter visited 40+ classrooms and noticed that the majority of students weren’t actively engaged in thinking during math lessons. This lack of engagement posed a significant barrier to effective learning. It became clear that fostering active thinking was essential for student success.

Identifying Non-Thinking Behaviors

Students often exhibited non-thinking behaviors, such as slacking, stalling, and mimicking. Mimicking, in particular was prevalent but ineffective for long-term growth. It became evident that tasks needed to be designed to encourage genuine cognitive engagement and discourage passive mimicry. This takes a change in practice as students are used to mimicking and communities look for study guides that mimic actual tests.  

Task Design for Access and Equity

To address these challenges, Peter mentioned to look for tasks with a “low floor, high ceiling” characteristic. These tasks are accessible to all students yet offer challenges for deeper understanding. Equity is often a primary goal, ensuring every student had access to meaningful learning opportunities regardless of their background or ability level.  While resources abound, they’re often underutilized or misapplied. Tasks needed to be novel and engaging to capture students’ interest and promote active thinking. Whiteboard tasks should give students opportunities to grapple with the math as an answer or specific process to solve hasn’t been given.

Strategies for Active Engagement

Peter noticed that Implementing BTC groups was a game-changer in promoting active engagement. By taking control away from teachers and making groups visibly random, most students felt included. Optimal group size was key, with groups of three proving to be most effective. Utilizing a visibily random process helped address issues of fairness and micro-bullying during group formation. That being said, I still frusturation on the faces of students when they find out they have been paired with someone outside of their peer group. I’ve gone the route of using playing cards, although the issues of students switching cards has been a problem during the last couple months.  

Challenges and Continued Growth

However, it’s important to note that negative student behaviors have impacted BTC groups. Addressing these behaviors has been an ongoing process throughout the year. By providing clear expectations and fostering a positive classroom culture, we’ve been able to mitigate some of challenges and create a more conducive learning environment.

My journey with BTC this school year has been rewarding with many ups and downs along the way.  Fortunately, I’ve had a great math team that has supported my efforts.  I’ve seen a noticeable improvement in my students’ mathematical communication skills and confidence compared to past years. This has been a journey and I look forward to seeing how it pans out for the last few months of the school year.

Still Building a Thinking Classroom

In the current school year, my team and I embarked on the journey of implementing Building Thinking Classroom (BTC) tasks. Our initial experiences were documented in a previous blog post. Since August, we have continued to employ strategies from the BTC framework, discovering valuable classroom practices while refining others through trial-and-error. This post provides a brief overview of our key practices.

Whiteboard Tasks:

Whiteboard BTC tasks, aligned with district-adopted resources, are assigned 2-3 times weekly. These tasks, sourced or created by team members (often put in a Google planning document), employ a playing cards method. Students are assigneda number corresponding to a specific whiteboard number. Students collaborate on the task for 10-15 minutes, utilizing a shared marker for each board.

Consolidation:

Upon completion (or work) of the whiteboard tasks, the class engages in two consolidation methods. Firstly, I guide the class to different boards, emphasizing diverse strategies. The class follows to the different boards during this time. Alternatively, students return to their desks for a seated discussion of the strategies on the boards. While both methods have shown promise, the latter has proven more effective due to increased student focus.

Pictures:

Following consolidation, students photograph their whiteboards, uploading the images to a Notability document. Adding captions to their pictures, students later submit them as assignments, fostering accountability and aiding in organizing their whiteboard tasks.

Checking Your Understanding:

Every 3-5 lessons, I administer assignments associated with a lesson group. This lessons are periodically worked on throughout the unit. On the due date, students review their work, compare it to a provided key, and make corrections using symbols like C, PC, or NY.

Notes to My Future Forgetful Self:

Aligned with the Checking Your Understanding assignments, Notes to My Future Forgetful Self tasks are completed independently by students. Submitted on Canvas, these notes and empahsis on vocabulary serve to review specific lesson sequences. Students sometimes include a picture of a BTC whiteboard task, providing insights in the form of captions.

Throughout the past months, our team has gained valuable insights into implementing BTC strategies. We have established a working routine and anticipate further integration of Peter’s ideas as the academic year progresses.

Reflecting on Building Thinking Classroom Routines

My middle school students have been in class for about two weeks. The first few days were spent creating a classroom community, completing name tents, and building norms related to expectations at the whiteboards. Over the two weeks students have worked on whiteboard around seven times. The first week it was all non-curriculular tasks and during the second the team shifted towards curricular-specific tasks – we are exploring area. The focus this year has been to start the year emphasizing strategies out of the Building Thinking Classrooms book. I believe classes are making progress with their whiteboard work and this post will summarize what’s been happening so far.

One of the first things that my team did related to whiteboard work was to create expectations for what was to happen during tasks. After non-curricular tasks students filled out this reflection sheet in a Desmos deck.

Students rated their engagement level and filled out a rubric. I reviewed the curated data with the class to help develop the norms, although I already had some ideas in mind. One of my math department team members found the below image while visiting social media communities related to BTC,

The ideas worked well with the norms that the class picked so we went with this. I posted a copy of this above image the whiteboards for students to reference.

For the most part, I’ve been following a similar routine with whiteboard tasks. This is a general routine and it varies depending on the lesson. Students enter the room, I take attendance, review the overarching goal, I give a brief mini-lesson on the topic and use a slide deck to introduce a specific topic. If the lesson involves manipulatives then we use them in our table groups to help build a better understanding on the topic. I then pass out playing cards ( I only use Ace-10) and show the task statement on the whiteboard. Students head to the whiteboards and begin working. The tasks last around 10 – 15 minutes before I ask them to send one spy out to review the work of others. Students return back to their groups and then finish up their work on the board. Usually I consolidate as a whole class and we visit different boards to review and reflect. Students take a picture of their whiteboard and put it in their math folder along with a caption in Notability. Then students fill a digital reflection sheet.

Wins:

Students are engaged in mathematical thinking . I’ve observed students talking with one another and debating ideas before putting the marker to whiteboard. That discussion seems to help students flesh out ideas and explain their thinking clear enough for their partners to understanding. Standing at the whiteboards seems to help student stay engaged more than sitting. Groups are sharing the markers. It didn’t start this way, but having one marker per group and sticking to that rule helps ensure that there’s more collaboration in the group as the ideas are spread. I’ve also noticed that students are increasing their mathematical thinking stamina while in groups – needed as students are now in middle school and the expecations are higher. Prolonged attempts at making sense of a problem and attempting a solution while in a group is more evident as students become more familiar with the whiteboard routines. I’ve also observed that students are becoming more comfortable with sharing their ideas with others when a spy comes to visit their group. When we first started sometimes students would hide their work. The ideas of knowledge mobility is becoming more common place and that’s a win.

Questions:

I still have questions though. Not everyone is on task and I still find some students distance themselves away from the group and allow others to do the heavy lifting. I noticed that some groups are waiting to complete all of their work untill a spy is sent out to retrieve hints or an answer. This has me questioning how often I send out the spy directions. I’m also still having issues with giving too many hints or asking students specifically direct questions to help move them in the right direction. Students are used to a different atmosphere in the math classroom so this is an adjustment. I’m aso working on becoming better during the consolidation process – especialliy when it comes to getting everyone back together and engaging in synthesis at the end of the whiteboard process. One last thing. My classes haven’t been assessed yet on the skills we’ve been addressing so I wonder how they’ll perform? My hope is that they’ll take what we’ve been learning and apply it thoroughly on the common assessment.

I’m looking forward to refining my own practice as the year continues. Feel free to ask questions or add your own experiences to this post. We’re all in this together!

Building Thinking Classrooms Conference

About a week ago, I had the opportunity to attend the Building Thinking Classrooms event in Indiana. The event spanned over two days and focused on the concepts explored in Peter’s book. Overall, the conference was refreshing and provided me with the chance to connect with fellow educators at my school. It had been a while since I last attended an in-person conference, so going with my colleagues was a refreshing experience. I believe that having this shared experience will prove beneficial as we embark on the new school year in approximately a month. I’ve had some time to process and re-read some of the book over the past week. I’m rejuvenating this blog and organizing my thoughts to translate them into actionable strategies when school resumes. Most of the ideas presented below are derived from the first few chapters of Peter’s book.

Defronting the Classroom

I have made significant changes to my classroom setup and design over the past few years. Instead of arranging students in rows, they now sit in groups, fostering greater collaboration. This shift has been particularly valuable since my district started implementing IM, which places emphasis on partner/group math discussions. I aim to maintain the group or pod structure but plan to alter the desk orientation so that the front of the classroom isn’t immediately apparent from the desk arrangement. I will position my desk near one of the middle sides of the classroom.

Visibly Random Groups

I also intend to continue utilizing random groups. In the past, I employed a digital method but I am now considering using playing cards as a means of determining the groups. Using actual playing cards will clearly indicate to students that the groups are genuinely random. By having predetermined groups, I hope to encourage students to collaborate and alleviate the cognitive burden of searching for a partner, considering the significant social aspect involved at the middle school level. Groups of three students tend to work well for middle school so that will be my plan for next year.

Vertical Whiteboards

In my previous classroom, I had several whiteboards that covered the perimeter. These whiteboards were fashioned by cutting two shower boards from Home Depot in half. While they have served me well over the years, I haven’t consistently utilized them. I aim to establish a few protocols before students use the whiteboards in the fall. My plan is to allocate one marker per group and co-create norms for using the whiteboard stations. These norms should encompass sharing knowledge by engaging students in gallery walks or sending someone to observe other boards. I need to remind students to show all their work and implement a system where they don’t erase (instead, they put a box around it and draw a single line through it) to encourage risk-taking and emphasize the process.

Observation Rubrics

I will involve students in co-creating norms within their groups which will eventually evolve into observation rubrics. I want students to evaluate the effectiveness of their groups. Although I’m unsure of the specific medium at this point, I am inclined towards a digital format that students can complete at designated intervals.

As I prepare to switch grade levels in the fall, I am excited about implementing the strategies mentioned above. The Building Thinking Classrooms event and Peter’s book have provided me with valuable insights and ideas that I’m eager to put into action. I look forward to this new adventure and the opportunities it presents for growth and learning in the upcoming school year.

Rounding Numbers

Over the past few years, my approach to teaching rounding has followed a similar path. The choice of methodology was often influenced by the adopted textbook within a school district. I would generally guide students to place numbers on a number line and determine their proximity to the nearest value. The class would focused on rounding to the nearest tens, gradually progressing to hundreds and eventually expanding to larger place values.

We would introduce a rule that involved underlining the digit to the right of the one being rounded. The rule states that if the underlined digit is “5 or more, round up; if it’s 4 or less, keep it the same.” I believe this has even been turned into a song at some point. This linear progression served as the foundation for teaching rounding at the early elementary level. 

This year brought about a change in our district as elementary teachers adopted a new resource. The emphasis shifted to exploring the value of numbers even before delving into the concept of rounding. Students were tasked with identifying the value of specific digits and ordering them, whether from greatest to least or vice versa. We incorporated the use of base-ten blocks and relied on expanded form extensively to help students develop a deeper understanding of number formation and the impact of place value on value itself. Students became more familiar with the value associated with each digit within a four or more digit number.

Students began identifying the closest multiple of a given number. For instance, they would determine the nearest multiple of 10,000 for a number like 432,000. This transition was seamless because students had already explored multiples and factors earlier in the year. Understanding how multiples relate to rounding was a novel approach and it resonated well with the students. Now, when asked to round to a specific digit, students consider the nearest multiple, which seems to make more sense to them. I am excited to continue using a similar rounding teaching strategy moving forward.

Assessment Retakes

Student assesment retakes have been a controversial topic among educators and parents alike. Some argue that giving students the opportunity to retake a test is necessary to ensure that they have mastered the material. This seems to be more prevalent around the circles that embrace standards-based practices. Others believe that it creates an atmosphere where students are not held accountable for their initial performance. I have seen first-hand how the idea of a retake plays a role in how students approach a test knowing they have a second attempt if the first goes awry.

There are several questions that must be addressed when considering implemeting as assessment retake policy. Where should students retake the test? Some schools may have designated retake days or a flex time, while others may allow students to retake the test during a designated study hall or after school. If it is after/before school, tranportation considerations need to be taken in to account. This can be an issue with invidividual teachers if no time exists for the retake. I know of some schools that build this “flex” time in to their master schedules while other schools leave it up to the teacher to decide if it happens.

Another important factor to consider is how much practice students should have before taking the retake. It is important to ensure that students have a thorough understanding of the material before retaking the test. This may involve additional practice materials or targeted review sessions with a teacher or someone else.

Additionally, it is important to determine how long the period should be between the initial assessment and the retake. Some schools may require a certain amount of time to pass before allowing students to retake the test, while others may allow students to retake the test immediately after receiving their initial grade. My thinking is that a certain amount of time is needed for error analysis and practice to occur before another attempt. Missing classtime for the retake can cause issues down the road.

Leaders should consider whether the retake policy should be implemented school-wide or on a classroom-by-classroom basis. Some schools may choose to have a consistent retake policy across all subjects and grades. Other districts or schools may leave it up to individual teachers to decide whether to allow retakes.

I believe the goal of any retake policy should be to promote student learning and achievement. I wrote about this same topic a few years back and am still refining my thiking on how to make retakes more effective.

Area and Math Mosaics

I believe that it is important for students to perceive math beyond mere digits on a page. Math is often seen as a subject that requires excessive computation, but it encompasses spatial reasoning and artistic aspects as well. Recently, I conducted a class where I blended the skill of multiplying unit fractions with creating a math mosaic and it turned out to be an enriching experience for the students.

To introduce the task, I collected different colored poster paper, glue sticks, scissors, and pencils. I divided the students into random groups and asked them to select an image that was traced onto the larger poster. The teams then decided on the colors and the quantity of each color required to complete the entire mosaic. Students estimated the amount needed and then used 1-2″ strips to find the exact amount. The gluing part of the project was the most time-consuming and required precision.

I was impressed by the critical thinking displayed by the students as they worked on the project. They were meticulous in their approach and made necessary edits to ensure that their work looked aesthetically pleasing. Most groups had to revise their total area numbers as well as number models. Additionally, the groups had to determine which medium to use to create their project, such as stone, tile, or glass. They calculated the entire amount required and added it to their total.

Once the project was completed, the class had a gallery walk where they examined all the creations. This project proved to be an excellent opportunity for students to practice their fraction multiplication skills while infusing an artistic element.

If you’re interested in exploring this specific project further, you can find detailed instructions by clicking here.

Transitioning Back to School

The first four school days of 2023 are officially in the books. This school year students and teachers had about 2 1/2 weeks off from school. Teachers came back for an institute day on Monday, and students returned on Tuesday. I find that every year, the transition from winter break back to a regular school routine can be rough. Students and teachers alike make a hard stop and transition back to commuting, eating at certain times, sustaining attention for a certain amount of time, and remembering expectations, etc. Having an institute day on Monday before the students arrived back was helpful in preparing to gradually move students back into school mode. The planning of the first few days reminded me of the first few days of school. They are actually similar in acclimating students to a routine, building a classroom community, and putting together expectations. I made an extended effort to build these in place as students entered the building on Tuesday. This post is primarily used to remind myself of what to do next school year and to share what seemed to work/didn’t work.

On Tuesday studetns came back and I gave time for them to discuss their break with their peers. Most of the students did not have a chance to talk with each other over break so this was a time to reconnect. After that students worked on filling out a 2023 reflection sheet that was created by @druinok.

Students had no problem coming up with 2 good things that happened in 2022 and 2 things that they were looking forward to in 2023. They had a bit of trouble with something to stop and the three goals. The class brainstormed a few ideas about what to stop and a common theme was procrastinating and having a positive attitude. Students then took the sheet and made a few edits after thinking it over. I mentioned that we will be revisiting this later in the school year.

After completing the sheet students added their responses to a Desmos deck that had similar questions. Students logged in using their Google credentials so I could provide feedback.

Students filled out the deck and confirmed their selection on slide seven. Later that evening I went into each submission and wrote a few comments.

One was related to what they did over break and the other was about their goal(s). Students reviewed the feedback the next day. I need to remind myself to do this next year as most students enjoyed this time and I was able to reconnect with them individually.

The second activity involved teams and involved blending math, puzzles and teamwork. Fortunately over break I found a terrific 2023 puzzle by @mathequalslove. I printed out the puzzle at home and tried it out. The “easy” puzzle was a perfect fit for my class as the pieces went horizontal and vertical. Students were randomly placed in groups and assigned the task of putting together the puzzle. I mentioned that the pieces could go horizontal or vertical. I didn’t realize that (or didn’t read it carefully enough) when I put it together at home and had to reach out to Sarah to find a solution. Some students had a challenging time putting together the puzzle. I had a few groups that thought it was impossible, but then they prevailed. Students cut out the final product, put a few designs on it and I put it on the wall. My hope is that when students see the wall it will bring back positive memories of persevering and working through a challenge.

The third task to help with the transition involved order of operations and collaboration. I have to give props to @seewins for putting together the 2023 year game challenge. I alwsy look forward to this amazing resource as Craig as been creating them for years.

Students worked in stations to find as many solutions as possible. The class worked on this for around 20 minutes and there were cheers when the class found a solution – talk about teamwork! I left the task open this week and some students even got their sibilings involved. One kid with the help of an older sibling was able to get 100.

On Friday students finished off the week by reflecting on the last four days. They reviewed their goal sheets and filled out a simple deck on how they were feeling.

The results indicated that many students were in the easy or not there yet. Only a few indicated that it was really tough. I believe we are making progress, but not fully in a routine yet. I feel like using activities like these mentioned inthe post has helped make the transition a bit easier and I will most likely use someting similar after long breaks moving forward.

Math Assessments and Self-Reflections

As 2022 ends I’m starting to think about next year. I’m now in the middle of a school break and reflecting on the progress that was made this past year. I’ve had some time to think about the last few weeks of school and what will come in January.

Before break my fifth grade students finished a unit on decimal multiplication and division. During the first three assessments I kept on finding that students made simple mistakes or didn’t completely answer questions before turning in the test. I feel like part of that is due to the increased staminia needed as we traversed from remote to hybird and eventually to in-person learning. The simple mistakes or incomplete work pieces were overlooked and impacted their marks – especially related to written mathematical responses.

To address this I decided to created a test checklist. The checklist included a line and a task. For example, __ I made an estimate before using an algorithm. The sheet was about 4″ x 4″ and printed out on colorful paper. All students filled out the sheet and checked-off each line before stapling it to the front of the test. I’d say most followed-through on checking and it reminded students to check their work in the process.

After the assessment I had students self-reflect on their performance. Students completed a Desmos task and here is the deck.

Students then checked-off correct vs incorrect answers. Students saw a list of concepts that might need bolstering and strength areas based on thier initial responses.

Students spent a good deal of time on this particular slide. They had to made a judgement call regarding where they were compared to the standard. Some students felt like they should’ve been placed in a different category because of a simple mistake. The next slide added an opportunity for students to provide context for their analysis or ask questions.

For the most part students found the process useful. I’m looking forward to using a similar self-reflection process for the next unit assessment.