October 2014 – Educational Aspirations

Exploring Rates – Part Two

exploringrates-01

One of the primary goals this year is to find opportunities to use rates in a more practical setting. This past week my classes started to explore rates in more detail. Students studied visual patterns and rules last week and this has led up to using/converting rates with formulas. While planning I dug out a rate activity that I used last year.

So on Monday I took masking tape and made a simple racetrack around the classroom. The track measured approximately 62 feet. Students took turns timing each other and documented how long it took them to quickly speed-walk around the track twice. We used an online stopwatch to time each student as they sped around the circuit.

Students documented their time and started to fill out the sheet below. The sheet is an upgrade from last year and I feel like it addresses more skills.

Students were asked to convert their time into feet per second and then how many feet would be traveled in one second. After the feet per second conversion, students converted the seconds to minutes. I gave students an opportunity to find this conversion by exploring and then checking their work.

Screen Shot 2014-10-24 at 9.35.26 PM

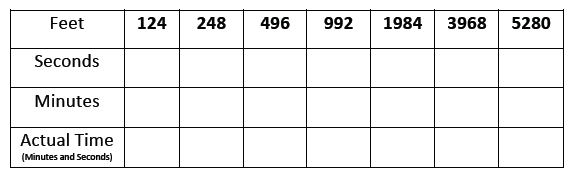
Similar to last year, this section was challenging for many. Understanding that 1.8 minutes isn’t 1:08 or 1:80 was addressed. I was proud to see students use perseverance to work through this section and use formulas to find solutions. The last section on the front asked students to find how long it would take for students to walk one mile at the 124 foot pace.

The most challenging part of this was converting the minutes and seconds to actual time. Once students understood the formula they became pros, or at least closer in understanding rates. Some even found how long it would take them to walk 5 and 10 miles. We shared the data as a class and found that our times per mile ranged from 9:45 – 16:00 per mile. Then students graphed the information on the backside. I actually thought of using a graph after reading through Fawn’s visual patterns template sheets.

Graphs

Afterwards, the class had a conversation about all the different math skills that were utilized while completing this activity. We made a list that included conversions, formulas, graphing and many others. I’m hoping to reference this activity and concepts experienced throughout the year.

Transitioning to the Standard Algorithm

When should the standard algorithm be introduced?

Many of my second grade classrooms are in the middle of their addition units. The classes often teach place value and addition strategies during the months of September and October. When introducing addition strategies, teachers rarely start using the standard addition algorithm (see # 4). Manipulatives and visual representations are heavily used during the first month of school. The process below differs per school, but I’m finding that this is often the case in many of the second grade classes that I’ve observed. Keep in mind that I’m missing other approaches, so perceive the following as a few highlighted strategies that are used during the first few months of school.

counters-01 — Finding the sum of objects

Students are introduced to some from of unifix cubes or counters. Students are asked to compile the groups of counters to find the sum. For the most part students find this task quickly and are ready to move onto the next portion. This is also a first grade skill that’s reviewed at the beginning of second grade.

circle11-01 — Identifying numbers on the number line

The number line usually follows the counters. Sometimes the number line makes an appearance before the counters, but it’s usually afterwards. The number line is used extensively. Students are asked to find numbers on the number line. This builds number sense and an understanding of the reasonableness of an answer. Eventually students are asked to add numbers with hops showing the addition involved.

Find the sum of 25 and 15. — Find the sum of 25 and 20.

Base-ten blocks are then introduced to emphasize place value. Students are asked to combine base-ten blocks to find the sum. They are asked to find the sum of the base ten blocks and place them on the number line.

The four processes above aren’t necessarily mandates, but it’s found in the sequence of the textbook. I should mention that the same process is used with subtraction later in the year. What I’m finding is that there’s rarely a mention of using the standard addition algorithm to find the sum. I don’t necessarily think that’s a problem, but it raises the question of when should the algorithm be introduced? In what cases should the algorithm be introduced and is it only used in certain circumstances.

Think of 200 + 198. Would your students use the standard algorithm for this? Some might, other might prefer to use another method. Regardless of when the standard algorithm is introduced, there will still be students that would prefer to use the algorithm. Is that the most efficient method?

The topic of this post was tackled during last Thursday’s #ElemMathChat. Most of the questions revolved around when the standard algorithm should be introduced and mistakes that occur when students focus on the steps. There were many useful answers, but I’m not positive if one right answer climbed its way to the top. There are many factors at play here. Some teachers feel pressured to move through the curriculum at a high pace because of testing. They might teach the algorithm sooner, while others might not mention it and scroll through the prescribed lesson sequence. Most teachers would like students to have a conceptual understanding of numbers and systems before moving towards a standard algorithm. How much time is spent developing that truly depends on the teacher and student. I’m not judging any teacher is these situations as we are all in this together, but I believe having this discussion is important. I think this also plays a role in how other algorithms are introduced.

Exploring Rules and Patterns

exploringrulesandpatterns

This past week my upper elementary classes started their equations, patterns, and rules units. The units are composed of patterns, special cases, student-created rules, and solving equations. To be honest this is one of my favorite units and involves a good amount of pattern exploration. Through exploration, students construct their own understanding of how mathematical rules can be developed by analyzing patterns. Many of these activities involve manipulatives or visual representations of various patterns. I’m going to highlight three specific activities that seemed to work well this past week.

Analyzing the Perimeter

Students were given a handful of square geometry blocks. They were asked to find the perimeter of one block. This was quick as students just needed to count the sides of the block. Four! Students then put together two blocks and found that the perimeter didn’t double, instead it was six. Students continued the patterns and discussed with their group what the rule could possible be. Some groups used the whiteboards to write possible solutions. Throughout this activity students struggled at first and then came to an understanding that the rule just didn’t include one operation. After the rule was discovered the students found the perimeter of 100, 200, and even 1,000 squares put together in a horizontal row. I believe this activity also helped establish the reason for having mathematical rules.

Rule Tables

Students used four dice, a whiteboard, iPad, and dry erase marker to complete this activity. Two of the dice were operation and they had + and – on the sides. The other two were typical six-sided 1-6 dice. Students rolled all four dice and created a rule. For example, if a student rolled a 6, 2, +, and – then he/she could say the rule is + 6 – 2. Students wrote the rule on top of the whiteboard and used one of the die to roll five numbers that would be included in the in column. Afterwards, students were asked to find the out column using the rule that was created. A few examples are below.

studentrules

The students then took a picture of their product and sent it to Showbie. Later on that day the class discussed how to combine rules. So instead of + 6 – 1 this rule could be + 5. The students were then combining all of their rules. This activity led to some productive discussions on how to simplify or expand rules.

Visual Patterns

visualpatterns

I came across Fawn’s Visualpatterns site a couple years ago. This is a fantastic resource that I introduced this past week. I printed out some of the patterns and placed them in manilla file folders. The picture of that is located near the top of this post. The six folders were placed around the classroom. Student groups visited each folder and determined the rule. While in the group students worked together and filled out the sheet below.

Screen Shot 2014-10-11 at 8.44.25 AM — Modified from this site.

Students took whiteboards and started to build possible rules for the pattern. Once they accomplished this they filled out the table and graphed the relationship. I appreciate that students are asked to graph their findings. This could lead into so many other math topics. Students only rotated through two folder stations so we’ll continue this activity next week. By the way, the students were stoked when I showed them the visual patterns site and not because it has the answers. A few students even said they were going to check out the other patterns on the site. I’m looking forward to utilizing this resource a bit more next week.

How do you introduce patterns, rules, and equations?

Assessments and Growth Mindset

8081867203_7ce422a6f5_z

School has been in session for over month and many of my classes had a unit assessment last week. The district adopted math program has 10-12 unit checkpoints (depending on the grade level) for the school year and each assessment covers specified math strands. These assessments are designed to assess understanding and include an open response that emphasizes students’ conceptual understanding and math communication skills. The entire unit assessment takes about 50+ minutes to complete.

I usually try to administer and grade all the tests on the same day. This doesn’t always happen. Before passing the tests back to the students the class generally has a discussion about certain problems that were missed more than others.

Screen Shot 2014-10-04 at 7.14.33 AM — What’s up with problem eight ?

We also have celebrations as a class. During the class discussion we don’t blame, but reflect on what the numbers might mean. This idea has taken time to cement and required a bit of modeling. Based on the results I might even teach a brief mini lesson to help address and reduce misconceptions. This is also an opportunity for students to analyze their own test and look for correlations. Afterwards, students are given a sheet to reflect on their own analysis. Students are asked to review their assessment and give feedback on their own performance.

Screen Shot 2014-10-04 at 7.23.50 AM — Click for file

After the students fill out the above sheet they visit the teacher for a brief conference. These last a quick 2-3 minutes and include a time to check-in with the student. We have a conversation about the student’s reflection and look for opportunities to improve in the future. This is also a time to set some possible goals. The sheet is glued into the student’s math journal and can be a document that the student will look back on as the year progresses.

I feel like the process of analyzing, reflecting and setting goals is important. I believe it reinforces a growth mindset mentality, but it also has me wondering about the role of different assessments in the learning process. I’d say about 95% of what is used at the elementary level is formative. I could see how that changes as students progress through middle and high school. Feedback and the possibility to make positive strides towards improvement can often be utilized with most assessments, regardless if you label it formative or summative. If a school truly embraces a growth mindset model, what role do summative assessments play? I believe that summative assessments have a role. I’m just thinking that they may be perceived a bit differently if a school emphasizes a growth mindset model.

image credit: Woodley Wonderworks