
My third grade students explored different addition and subtraction algorithms this week. It’s been a challenge. In the past, students used number lines to add or subtract by the highest place value first and then slowly move towards the lowest. Moving towards a standard algorithm has been a process this week. Students started by using the partial-sums method. This was similar to what they were used to and mimicked the number line models. Students seemed fairly comfortable in using this method. The column addition method was next on the docket.
Many students come into my classroom already knowing how to use this method. It’s often referred to as the traditional/standard addition algorithm. Students complete the steps and out comes an answer. Does it make mathematical sense to my third graders? In some cases the answer is no. So, in an effort to bring a bit more meaning to why it works I decided to use a code activity to reinforce the idea of base-ten and place value.
Cracking the muffin code is an activity found in the Everyday Day math curriculum. A quick Google search will also bring up many different threads related to this activity. I’ll be paraphrasing the lesson throughout the post. Basically, students are given a scenario where they’re in charge of a muffin market. At the market the muffins are packed into boxes. The boxes only hold a certain amount of muffins. When someone asks for muffins, an employee fills out an order form. That order form contains a code. The largest box needs to be filled first and the employee needs to send boxes that are full. Here’s an example that I paraphrased from class:
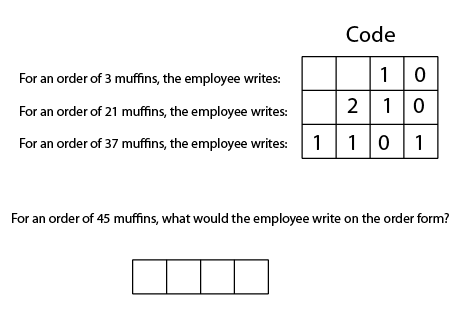
I had students work in groups to figure out the code. I gave them around 10 minutes and at the end of time a few groups were fairly confident with their answer. We discussed the code and students started to notice a pattern. They used trial-and-error to figure out which column matched the box size.

There was a lot of excitement in the air as students solved the puzzle. Afterwards, students connected this to the idea to place value for the next problem. This puzzle was designed differently. Now, students were asked to pack boxes of granola bars. The packages hold 100, 10, or 1 bars. The employee uses a coding system. Here’s another example:

Almost immediately, students were able to see that the first column was designed to package one bar. The second was for ten, and the third, one hundred. I gave time for students to look at the similarities and differences between the granola and muffin codes. Students were then asked if the base-ten system was similar to the granola code. Students nodded their heads and I even had a student say that when we regroup numbersit’s like adding another package. Another student stated that sometimes not all the numbers fit in a package so we have to find another place for them. Students were making connections to how the base-ten number system works and why regrouping is sometimes necessary.
This was an eye-opening experience for some students as they started to look at the place value positions as bins or containers. This lesson had students talking about how place value can be perceived as “containers” or “boxes” for numbers. Each box needs to be filled to it’s capacity until a new one can be used. I’ll be referring to this activity throughout the year as it seemed to help students make connections when exploring the base-ten system.
Afterwards, students used the column addition algorithm with a bit more confidence. Next week we’ll be discussing multidigit subtraction.
Makes me want to make up a number system that isn’t exponential — just has different package sizes 🙂
LikeLike
HaHa. This activity did lead to some discussion about numbers and why we use the current system.
LikeLike