Matt Coaty

Math and Sports

To be honest, it was a memorable Superbowl game last night. Watching the game brought back many memories from past professional sports games, specifically the Chicago Bulls dynasty in the 1990s. One memory that caught up with me dealt with middle school math. I started to enjoy math in middle school. I started to view sports as percentages, ratios, and decimals. This started my journey in appreciating math. Most of my students watched the Superbowl and I think that this is a great opportunity to delve into statistics as well as data analysis concepts in the classroom.

Let’s take Eli Manning as an example ….

*All of the football images and statistics were found on Wikipedia

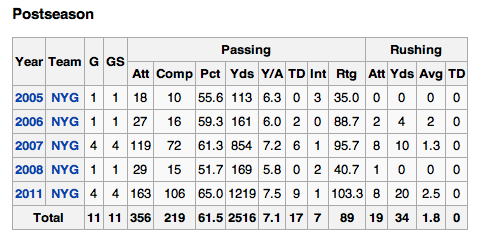
Let’s take a look at Eli’s statistics:

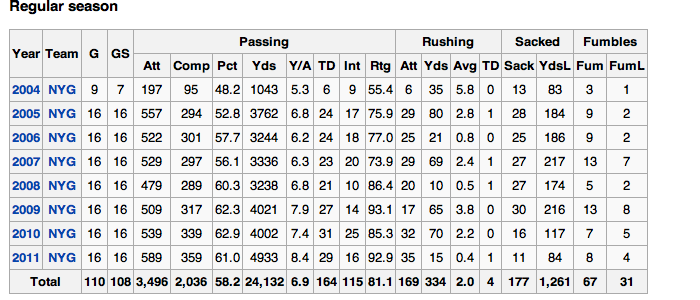
Using Eli Manning’s statistics, we can view trend data. Here are some questions to ask the students:

How many yards do you think Eli will pass for next year?
How many games do you think Eli will play next year?
Predict Eli’s passing rating for the 2012 season? Explain your prediction.
Do you notice any trends? If so, can you explain why the trends exist?

After asking the questions above, we can take a gander at Eli’s post season statistics.

Compare Eli’s regular season and post season performances.

What differences do you see in the data?
What do you think contributes to a quarterback rating. Why?
Using the data, what factors do you think impact a quarterback rating?

After discussing the questions, you may want to have a conversation how statistics often relate to percentages.

Additional Sports and Math Links:

Dice Game

NFL Probability

Math and Football

Incorporating Sports into Math

Velocity in Sports

Math in Sports PowerPoint

Math and Sports Webquest

Wanted: Math Skills for Discounts

Image by: A. Balaraman

I recently came across “Number Crunching Coupon Calculating Champ” on a Facebook page. The screenshot image is found below. I plan on incorporating this page into my math instruction next week. According to the website, if I completed the problem correctly I would receive a certain percentage off of my next purchase. So … completing a math problem on the Internet = a percentage discount? I don’t recall ever reading a promotion like this before. Regardless of the motivation behind the company sponsoring the ad, I thought this type of math application could benefit my classroom.

I didn’t fill out the form, but I thought that this type of problem could possibly supplement my instruction. There are many ways to teach discounts, but real life examples bring awareness that math is everywhere.

There are many different ways to solve this type of problem. I may have the students work in collaborative groups to find the answer. All of the different mathematical operations will be useful to practice. Overall, I feel as though this type of problem will give students an opportunity to utilize their mathematical knowledge in a practical way.

My students enjoyed working out the problem above, although it is quite intense for an elementary student. The picture below might assist in starting a discussion about percent increases and the processes involved in finding the answer.

%increase — What is the percent increase from 7 to 10?

Fundamental Place Value

Image by: D. Castillo

After analyzing a recent math assessment, I asked a group of middle school teachers in another state what particular math topic they would recommend elementary teachers strengthen. I thought that the middle school teachers could offer valuable input regarding how the elementary schools are preparing students for middle school. After a quick discussion, each middle school teacher (all five of them) decided that place value is a fundamental concept that precedes many other high-level math concepts. After listening to the discussion, I started to think of when place value is actually taught. According to the math Common Core, an entire math strand is dedicated to place value / base 10 concepts. In fact the word place value is found 42 times in the Common Core Standards for Mathematics. Obviously, place value is important, but how do teachers introduce and expand on the topic? First of all, teachers can use visuals,such as a place value chart.

Ideas and links regarding teaching place value can be found below.

Place value can start before first grade – counting and identifying specific values
Students can be given the opportunity to utilize base-ten blocks and explore how the pieces are interchangeable
Place value can be viewed as a decimal or fraction
Use coins to show another way to view place value
Tactual place value activities
Online games or activities
Use a number line to show how place value plays a role in how large or small numbers become.

Reflection Journals in Math Class?

Image by: Samana

In the past, I’ve used reflection journals for language arts assignments. Allowing students to reflect via journaling was one way that I could informally assess whether students were making connections to the literature. After utilizing the idea of journaling for my language arts class, I thought that it might be useful to integrate this strategy with math. Before starting this adventure I decided to complete some homework on the idea of math journaling. In the past I’ve used standard reflection sheets. While collecting ideas, I also looked for math journal writing prompts and rubrics 1 2 3 . I found many ideas and strategies for math journaling here and at Monica’s website. If you’re unsure of how to introduce the topic of math journaling, this Word example may help. If you’re curious of where to start, I’ve found that this site provides terrific examples. So, after researching a few options I decided to label all of my journals and prepare for uncharted territory.

After giving a unit assessment, I gave my first math writing prompt:

How do you feel about your performance on the last unit assessment?
What type of math concepts do you find interesting? Why?

Students were also asked to include a picture with their response. Why a picture? I thought that allowing students to draw a picture may portray how they feel regarding their performance. Some students decided to draw more of a picture, while others decided to write more with words. Allowing this type of flexibility gave students an opportunity to communicate their response to the writing prompts differently. The students then turned in their journals and I wrote a short response to each individual response. I feel as though the students really enjoy the fact that I personalize my response to each student. I also feel as though this builds a positive classroom environment, as each student is shown that their opinion is valued. The journals can also be used during parent teacher conferences, although it might be a good idea to disclose this to the students before they write.

What happend?

After completing a plus/delta chart, students thoroughly agreed that the math journals enabled them to reflect on how they are doing in the class. Some students even communicated that the journals were a way to set specific math goals. Currently, I give students an opportunity to complete a journal entry approximately every two weeks. A byproduct of using the journals may also lead to personal goal setting and more academic involvement from the student.

What’s next?

I would like to incorporate the idea of utilizing specific math vocabulary in the journals. Not only should the math journals be used for reflection, but they can also be used as another opportunity to practice mathematical concepts. As an elementary school teacher, I think it’s important for students to have a solid understanding of math vocabulary at a young age. Having consistent definitions is also important. Certain math vocabulary words that are utilized in first grade will accompany a student throughout their entire life. For example: multiply, divide, sum, fraction, etc. Overall, I feel that students will become better at understanding math vocabulary and reflect on their learning through the math journals. The journals will be used consistenly, so students will observe the progress that they have personally achieved throughout the year.

Geometry Birds

Most teachers would agree that making math relevant and engaging is important. Utilizing student interest in a math lesson can turn a good lesson into a great lesson. Moreover, the lesson will be memorable for the student – even after the assessment. An example of this type of lesson can be found here. Over the past year I’ve seen many Twitter posts (and publication articles) regarding how to use Angry Birds in the classroom. I understand that this game can be used for a physics discussion, but since I teach at the elementary level, I often skimmed those types of posts and looked for some type of way to integrate this extremely popular game into my classroom.

Even at the elementary level, students are intrigued and can tell me all about the game itself, from strategy to cheat codes. I feel that part of my job is to engage students in meaningful learning. Last weekend I came across a blog that led to this site that shows how Angry Birds can be used to teach geometry concepts at the elementary level. The site even had colorful PDFs that I could print to make this activity realistic. I utilized this activity for my third grade class.

Here are the steps:

1.) I printed out the PDFs and had my students create all of the different geometric solids. Here are the pdfs (1) (2).

2.) I showed students different types of solids. I also brought out the manipulatives found below.

3.) I then reviewed the following vocabulary words: vertices, faces, edges, and surface area.

4.) Students were given an opportunity to pick the net of one particular bird. Here’s an example:

5.) Students used scissors and glue sticks to build their particular bird.

6.) Once finished, students were asked to fill out an exit card regarding the amount of edges, vertices, and faces of the particular bird that they created.

7.) The birds were then posted in the classroom. The pictures are below.

Math Curiosity

http://www.youtube.com/watch?v=cdRCfxpZ8b4&feature=player_embedded

Image by: Samana

Here’s a typical elementary multiplication math problem:

John has 5 buckets with 10 tomatoes in each bucket. How many tomatoes does John have in all?

To be honest … there’s nothing really wrong with the problem, but there are different ways to teach multiplication. To me, this type of problem, although it could happen outside of the classroom, seems extremely scripted. I’ll tell you a quick story about one of my math lessons from last week.

Last week I was given the opportunity to teach second and third grade students multiplication. I find that when students are able to explore their own curiosity regarding math, they are often more intrinsically motivated to learn. I’ve attempted to create a classroom environment that promotes math curiosity. After introducing students to the idea of multiplication, I showed the students the video below.

After watching the video, I posted a few follow up questions on the whiteboard. The class had a thorough discussion foru about 15-20 minutes regarding the mistakes made by some of the actors in the video. Students where asked to answer the questions below in collaborative groups and eventually communicate their answers to the class. Here are a few of the questions:

1. What math vocabulary terms did you hear/watch in this video?

2. Did you see any math mistakes? If so, where?

3. Could some of the mistakes be prevented? if so, how?

4. What was done correctly?

5. How can you prove that your answer to a multiplication problem is correct?

6. What can we learn from this video?

Overall, I thought this was a great supplement to a multiplication lesson at the elementary level. Integrating technology and asking thought provoking questions gives students opportunities to follow their curiosity.

Is Math Linear?

Some Twitter users suggest that math isn’t always linear. The curriculum that math teachers teach may resemble something linear, although some curricula (example: Chicago Everyday Mathematics) may engage in some type of spiraling format. Even if a curriculum spirals, it is still somewhat linear. Most teachers would suggest that background knowledge is needed to learn higher level concepts. This is especially the case at the elementary level. Generally, teachers are expected to teach specific math concepts at certain grade levels. Most of these concepts are assessed by the state for that particular grade level.

This past week I was teaching a math session with a group of upper elementary students. We were having a conversation regarding triangles and angles. We covered the topic that the measures of the interior angles should equal 180 degrees. One of my students then asked how do we find an unknown side of a triangle. I thought that was a decent question, so we took out our math books and started looking for clues in the geometry section. The book led us to a dead end. So … I thought of my own learning and remembered something about the Pythagorean Theorem helping with this question. As a class, we traveled on the internet and Googled Pythagorean Theorem.

We explored the following pages:

http://en.wikipedia.org/wiki/Pythagorean_theorem

http://jwilson.coe.uga.edu/emt669/student.folders/morris.stephanie/emt.669/essay.1/pythagorean.html

http://www.pbs.org/wgbh/nova/proof/puzzle/use.html

http://www.teachscienceandmath.com/2010/03/03/pythagorean-theorem-real-world-application/

After digging up a few resources, we finally found a group of students that created a short video on the Pythagorean Theorem.

After reviewing the video above we decided to practice a few problems using our new knowledge. The students seemed to enjoy and were motivated to continue on this Pythagorean adventure. I asked the students to research the Pythagorean Theorem that evening and practice a few practical problems. I also asked them to bring in any practical problems relating to the theorem to school the next day. The next day the students came in with papers of practiced problems and examples. Overall, I felt as though this was a great opportunity to expose the students to a higher level skill, that isn’t necessarily linear, but may benefit them in preparing for middle school.

Multiplication Fundamentals

Image by: David Dominici

Learning the fundamentals of a particular subject area is important. In the realm of math, the word fundamentals can be misleading. CNN produced an article on the lack of math fundamentals in this piece. Every math strand requires some type of fundamental understanding. According to the Core Standards, mastering the multiplication tables should occur in the early elementary grades. Having mathematical fluency at a young age is important. In elementary school, students that haven’t mastered their multiplication tables may fall behind and not be able to access higher level math skills that require a concrete understanding of multiplication. Beyond raw memorization via flash cards, teachers need to find strategies/methods to introduce the multiplication tables. Over time, I have found that the following strategies enable students to understand and master the multiplication tables (0-10):

1.) Math Apps

The following apps help students master and deepen their understanding of multiplication:

– MathBlaster Hyperblast

– Math Ninja HD

– Rocket Math

– Factor Samurai

2.) Manipulatives

Students often need a visual demonstration to come to their own understand of multiplication.

– Egg Carton Math

– Multiplication Balloon (Could easily be created)

– Base Ten Multiplication

3.) Games

– Math Smart Game (Students could actually create their own multiplication board game)

– Multiplication Four in a Row

– Multiplication / Factor Bingo

4.) Student Multiplication Projects

– Multiplication House

– Math Wanted Poster

– Multiplication String Art

5.) Introducing Practical Multiplication Problems

Finding practical math problems is important and gives students an opportunity to apply their learning. Here are a few resources that may introduce problems or communicate the relevancy of using multiplication outside of the classroom.

Real World Math Problems (PDF, Word, and PPT forms)

Elementary Multiplication Examples

Geography and Multiplication (PDF)

Additional Multiplication Resources

IBM Youtube Commerical (Why is math relevant?)

Make a Math and Art Connection

Transforming Professional Development for Teachers

Image by: David Dominici

I recently was looking for some space in my closet and found a book from my graduate school days. The book Transformational Leadership & Decision Making in Schools by Brower and Balch fell out of my closet.

After flipping through the some tabbed pages, a few memories emerged. One of the chapter topics explained how ed. leaders often understand and create effective professional development opportunities for their staff. Understanding what is considered “effective” is key. So I ask, what is needed for effective staff development?

Three (non-exhaustive) Ideas for Staff Development:

1.) Eliminate fear – As discussed in David’s post, teachers shouldn’t feel as though someone will steal or reject their innovative ideas. Competition, although beneficial in some scenarios, may instill in teachers a sense of fear and distrust. Administrators that advocate for their staff members by creating an atmosphere of trust and collaboration often improve student learning over time. The idea that all of the students in a school are everyone’s responsibility should be prevalent and community building activities indicating that concept should be evident.

2.) Research Based PD – Often, staff development may meet the current needs of the staff, but not necessarily be research based. Many PD sessions are more “training” focused, rather than “best practice” focused. This point is explained in more detail in Neil’s post. Teachers need to be able to understand that the PD sessions, when implemented appropriately will result in an improved organization.

3.) Follow up – Ask any educator … it’s fulfilling to participate in an effective PD session. The question that many people have after the session is … Now What? Allowing time for teachers to collaborate and discuss methods to implement ideas will benefit all stakeholders. Also, it may be important to receive feedback from the audience (teachers) in order to measure the effectiveness of the PD and set goals for planning additional sessions.

Disclaimer (unfortunate but necessary) : The thoughts and opinions expressed in these pages are my own, and not necessarily the opinions of my employers.

The Real Number Line – In Practice

Image by: Samana

A little while back I wrote a blog post about how the typical math number line needs an upgrade. You can find that post here. I thought and still think that the general math number line that is introduced at the elementary level needs to be enhanced.

I believe that students should encounter all types of numbers on a number line. Students should find whole numbers, decimals, square roots, fractions, percentages, mixed numbers, etc. Of course, the concept needs to be age appropriate . So, in my last post I wrote about how students should understand the real math number line. In theory it sounded like an idea that could be put into practice. I decided to find out how the theory looked in practice. I asked students to create a math number line with multiple components. This activity fit in well with the decimal and fraction unit that I’m currently teaching. I gave each student learning group a sheet like the one below and a specific number range (like numbers 3 – 6).

Every student worked on this project in a cooperative group. Through this experience, I believe the students had a unique opportunity to learn about the many different ways that numbers can be represented. See below for examples.

Overall, students were engaged and thoroughly enjoyed the activity. At the end of the project, I facilitated an informal plus/delta chart and the feedback was generally positive. While students were in their cooperative groups I overheard them debate the differences and similarities of fractions, square roots, decimals, improper fractions, and mixed numbers on the number line. It was a great learning experience and definitely a project I’ll put in the plan book for next year.

Disclaimer (unfortunate but necessary) : The thoughts and opinions expressed in these pages are my own, and not necessarily the opinions of my employers.