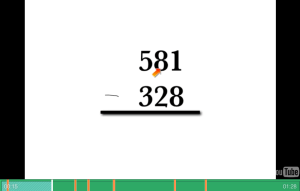
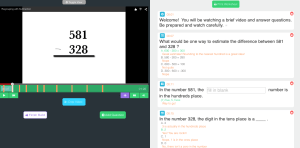
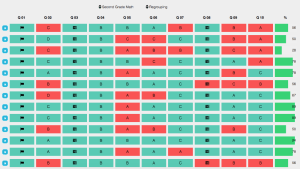
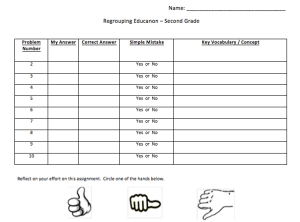
Over the past week I had time to disconnect a bit and spend time with family. I was able to stay with relatives in another state and spent most of the time catching up with people I haven’t seen in a while. It was a great time to refresh and reflect on the past year. While relaxing one relative in particular asked me about this “new” math that’s in the schools now. I was asked why schools are changing how they teach math and why it needed to change. Specifically she spoke of the different strategies used to compute numbers. I’m assuming she meant the extensive use of the number line and compatible numbers. I defended the reasons for a more conceptual understanding of mathematics, especially at the elementary level. Many of the “new” strategies help build that understanding and enable students in developing a foundational understanding of numbers. The relative was receptive and asked more questions related to this topic. I felt like her understanding of the topic became clearer as we discussed the use of multiple strategies utilized to teach computation. This was a small part of our longer conversation, but the topic had me thinking about how to provide opportunities to address misconceptions. In particular, I thought how my conversation could apply to addressing math misconceptions in schools.
I feel like one of the more important issues with student misconceptions stems from a lack of addressing them. They tend pile up and build over time. I vaguely remember having a math teacher that asked if his students had any questions. I remember looking around and wondering if I was the only one in the class that had multiple questions. Unfortunately I kept my hand down even though I was lost. The teacher then quickly surveyed the room and seeing that no one had their hands up, moved onto the next topic. I found that the less I asked questions that less comfortable I was with the current concept and the process continued until I finished the class. Looking back, I’m sure there were other opportunities to address my misconceptions and questions; I just don’t remember any of them at the time of this writing. I didn’t learn as much as I should from the class, but I started to understand that I needed additional opportunities to ask clarifying questions.
In addition to including many opportunities to address misconceptions, the classroom environment plays a pivotal role in having students feel comfortable in offering input. The strategies below can be used in a variety of settings. I’ve had success with the strategies, although some have been more successful than others.
Classroom Math Conversations
Classroom conversations can be a powerful strategy in gaining a better understanding of students’ viewpoints. Using open-ended math question and having groups respond to the class can offer opportunities for a healthy math debate. For example, I’ve seen some teachers use Always, Sometimes, Never with great success. Math Talks can also be an avenue in which classroom conversations can develop. Through these conversations teachers can glean important information and possibly misconceptions that can be addressed later or at that time. These types of math conversations, accompanied with anchor charts can document the classroom’s learning journey. The anchor charts can then be revisited as students construct their understanding.
Formative Assessments
These types of assessments can take different forms. Some teachers prefer to use exit cards, while others use a quiz model. Formative assessments can be used via technology means and some may take the form of a paper/pencil quiz. Regardless of the form, the student’s response can give teachers an indication of understanding. In order for the teacher to give feedback the question needs to be appropriate. Students need to be given the opportunity to explain their reasoning or steps involved in solving problems. If not, the problem is wrong/right, and the teacher is unaware of where the mishap is occurring. Using written or verbal feedback to address the misconception can lead to a more in-depth conversation at a later time. Some students may need the reinforced conversations while others may not. I believe most teachers understand their students and at what level to scaffold feedback.
Journaling
Similar to answering a question in a classroom student group, journaling can provide students a low-risk venue to showcase their understanding. Through a prompt, math journaling can allow students to explain their mathematical thinking and processes in a written form. Students often become more aware of their growth as the year progresses. I find that students might not know that they have a misconception until it’s brought to light. It’s the you don’t know what you don’t know dilemma. The concept of math journaling can be used for teachers to write feedback to individual students and ask questions that give students opportunities to reflect on their writing and math process. Allowing a bit of extra time to confer with a student after their math journaling process can be beneficial as teachers may want to review specific concepts with students.
All of these strategies above seem to go well with a heavy dose of teacher feedback and student self-reflection. Through reflection, students can help internalize and address the misconceptions.
How do you address misconceptions in the math classroom?