Math Instruction – Page 21 – Educational Aspirations

Math: In Response to Your Question

I’ve been exploring the use of multiple solution problems in my math classes. These types of problems often ask students to think critically and explain their mathematical processes thoroughly. To be honest, these questions can be challenging for elementary students. Most younger students expect or have been accustomed to finding one right answer throughout their academic career. Unfortunately, state and local standardized assessments often encourage this type of behavior through multiple choice questions. This type of answer hunting can lead to limited explanations and more of a focus on only one mathematical strategy, therefore emphasizing test-taking strategies. Encouraging students to hunt for only the answer often becomes a detriment to the learning process over time. Moving beyond getting the one right answer should be encouraged and modeled. Bruce Ferrington’s post on quality over quantity displays how the Japanese encourage multiple solutions and strategies to solve problems. This type of instruction seems to delve more into the problem solving properties of mathematics. Using this model, I decided to do something similar with my students.

I gave the following problem to the students:

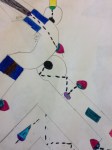
How do you find the area of the octagon below? Explain the steps and formulas that you used to solve the problem.

At first many students had questions. The questions started out as procedural direction clarification and then started down the path of a) how much writing is required? b) how many points is this worth? c) how many steps are involved? d) Is there one right answer? I eventually stopped the class and asked them to explain their method to find the area of the octagon, basically restating the question. I also mentioned that they could use any of the formulas that we’ve discussed in class. Still, more questions ensued. Instead of answering their questions, I decided to propose a question back to them inorder to encourage independent mathematical thinking. Here are a few of the Q and A’s that took place:

SQ = Student Question TA = Teacher Answer

SQ: Where do I start?

TA: What formulas have you learned that will help you in this problem?

SQ: Do I need to solve for x?

TA: Does the question ask for you to solve for x?

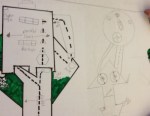
SQ: Should I split up the octagon into different parts?

TA: Do you think splitting up the octagon will help you?

SQ: How do I know if the triangle is a right angle?

TA: What have we learned about angle properties to help you answer that question?

Eventually, students began to think more about the mathematical process and less about finding an exact answer. This evolution in problem solving was inspiring. Students began to ask less questions and explain more of their thinking on paper. At the end of the math session students were asked to present their answers. It became apparent that there were multiple methods to solve the problem. Even more important, students started to understand that their perseverance was contributing to their success. The answer in itself was not the main goal, but the mathematical thinking was emphasized throughout the process.

Afterwards, students were asked to complete a math journal entry on how they felt about the activity.

Image Credit: Kreeti

Taking Math Outdoors

Recently I had an opportunity to attend an outdoor education trip with our elementary students. The trip took place over three days and was located in a very remote part of the state, away from high rises, city lights, cell phone signals, and televisions. The trip focused on learning about birding, forest ecology, Native Americans, orienteering, and pioneering. For many students this trip is a different learning experience. It’s outside of the classroom and therefore a different learning environment for them. Acclimating to this environment took a bit of time for staff and students.

The adults were responsible to teach many of the concepts during hikes on campus. Being outside is a great opportunity to introduce or highlight academic concepts that are generally taught through abstract means. While talking about math outdoors, students expressed interest and asked questions that often led to additional mathematical questions. Students that might not usually be fully engaged in a math lesson at school were shining on the hike. This experience led me to reflect on our current mathematical practices. At times there’s a disconnect between what’s happening in the classroom and what’s occurring right outside of the doors to the school. Teachers often attempt to bridge the gap, but self-directed student questions often come from real world experiences and curiosity. Curiosity is often followed by questions. Finding answers to those questions can lead students to find their passions (eg. #geniushour). This motivation can be encouraged but not genuinely bought or sold. Students decide how engaged they want to be and internal/intrinsic motivation often leads to learning experiences.

Below are some (of what I can remember) of the questions/topics that were discussed while on the trip:

Math Debates in Elementary Classrooms

Over the past few months I’ve dedicated a good amount of time to to having math conversations. These math conversations occur when the class is unsure of how to solve a problem or when disagreement ensues over what particular strategy should be used to tackle a problem. The math conversations (or debates) allow students the freedom to openly discuss logical reasoning when solving particular problems. These conversations can be sparked by the daily math objective or follow another student’s response to a question. It’s not necessarily planned in my teacher planner as “math conversation” in yellow highlighter, but I do make time for these talks as I feel that they bring value and encourage student ownership. The conversations also give insight to whether students grasp concepts and are able to articulate their responses accordingly. Mathematical misconceptions can also be identified during this time.

During these conversations I have manipulatives, chart paper, whiteboards, iPads and computers nearby to assist in the discovery process. I emphasize that there’s a certain protocol that’s used when we have these discussions. Students are expected to be respectful and listen to the comments of their classmates. To make sure the class is on task I decide to have a specific time limit dedicated to these math conversations. Some days the conversation lasts 5 minutes, other days they may take upwards to 15-20 minutes. When applicable, I might use an anchor chart to display the progress that we’ve made in answering the questions. I should also mention that sometimes we don’t find an answer to the question. Here are a few questions (from students) that have started math conversations this year:

Why is regrouping necessary? (2nd grade)
What can’t we divide by zero? (3rd grade)
Why are parentheses used in math? (3rd grade)
Why do we need a decimal point? (1st grade)
When do we need to round numbers? (2nd grade)
Why is a number to the negative exponent have 1 as the numerator? (5th grade)
Why do you have to balance an equation? (5th grade)
How does the partial products multiplication strategy work? (3rd grade)
Why do you inverse the second fraction when dividing fractions? (5th grade)
Why is area squared and volume cubed? (4th grade)

Above is just a sampling of a few of the math conversations that we’ve had. Afterwards, students write in their journals about their experience finding the solution to the problem.

Of course this takes additional time in class, but I believe it’s time well spent. The Common Core Standards focus on depth of mathematical understanding, rather than breadth. This allows opportunities to have these conversations that I feel are beneficial. They also emphasize the standards of practice below.

CCSS.Math.Practice.MP1 – Making sense of problems and persevere in solving them.
CCSS.Math.Practice.MP3 – Construct viable arguments and critique the reasoning of others

Photo Credit: Basketman

Do you have math conversations in your class?

Equivalent Fractions Tweak

A few days ago I started gathering resources to supplement a math unit on fractions. The classroom was studying equivalent fractions and I thought there might be a variety of resources available on a few of the blogs that I regularly visit. I generally follow the #mathchat hashtag and find/share ideas that relate to mathematics. While reading a few math blogs on fractions, I came across John Golden’s site that has some amazing ideas that can be used in math classroom. His triangle pattern template sparked my interest.

John provided a template that’s available on his site. I printed out the template and began filling out each triangle with fractions. I ended up with a sheet that looked like this.

So what happened?

First a lot of brainstorming and error checking. Then I decided to have students cut out the triangles and compile equivalent fractions. This is what happened …

Students in fourth grade cut out each triangle and combined them to make equivalent fraction squares. Students worked in collaborative pairs during the project. I observed students using math vocabulary and having constructive conversations with each other to finish the assignment.

Before giving the assignment to a fifth grade class I decided to eliminate two triangles on the sheet above. It was the job of the student to find what triangles were missing and create equivalent fractions to complete the squares. The students were engaged in this activity from start to finish. Some students even wrote the equivalent decimal next to each square.

Overall this project took approximately 45 minutes to complete and it was worth every minute. Students used the terms fraction, improper fraction, mixed number, numerator, denominator, multiplication, division, and pattern throughout the project.

Just as I did, feel free to tweak this project to best meet the needs of your students.

Teaching Algebra Through a Different Lens

I recently taught a lesson on pan-balance equations. In my curriculum pan-balances are taught as a precursor to more in-depth pre-algebra. My students seemed to understand simple pan-balances and found that the balances (like an equation) needs to be balanced to work. The majority of students had no problem with questions (like these) involving oranges, apples, paperclips, etc.

Day Two

During the next lesson I introduced the idea of variables with equations, like 2x + 4 = 18. Students seemed to understand, but less than the first lesson. I brought everyone up to the classroom whiteboard and practiced many problems with the students. The students who understood always seemed to raise their hands, while students who didn’t completely grasp the concepts tried to blend in with the carpet. Students became less interested in what I was teaching when I started writing equations on the whiteboard. Unfortunately, I felt like I was losing a battle here. The more the students seemed to not understand, the more I felt the need for direct instruction. Near the end of the lesson around half of the students seemed confident to proceed to the next algebra lesson – solving for x on both sides of the equation.

I had to change something.

Day Three

During the next day I decided to change up my instructional approach. I remembered back to when I first learned algebra and the confusion that I used to experience. My school memories of algebra started and ended by watching a chalkboard and overhead projector, as my teacher wrote and erased equations on the board. This was the only way to learn algebra, or so I thought back then. Using my experience I decided to change the instructional medium.

I started my next algebra lesson with a quick review of pan-balances. Students seemed to gain confidence as we had a conversation about the importance of using algebra in careers outside of the classroom. We watched a quick BrainPop video on algebra and it’s uses. Instead of using the whiteboard again, I decided to take out the iPads. I already downloaded an app called Hands-On Equations a few weeks ago. The students were quickly motivated and I modeled how to use the app under the document camera.

The class and I went through a few problems together until I thought they were ready to proceed. I allowed the students 20 minutes to explore the app and lessons. The students were expected to complete at least three lessons and reflect on their experiences in their math journal. What was interesting was that the students immediately took control of their own learning and utilized the app at their own pace.

Payoff

After approximately 20 minutes, I asked the students to write in their journal how they felt about their journey with pre-algebra. The majority of responses were positive …

“I now understand why we use algebra”

“I never thought algebra could be so much fun”

“Having a picture of the balances helps me understand the concepts better.”

The Takeaway …

After hearing their responses and reflecting on the outcomes, I’m becoming more motivated to vary instruction to better meet the needs of my students. Varying the instructional approach can give students multiple opportunities to grasp concepts that can be particularly challenging. Your students may benefit from a bit of instructional change from time to time.

photo credit: ajaxofsalamis via photopin cc

Dice and Math Computation

Since the beginning of the school year I’ve been searching for different ways to incorporate guided math in my classroom. Guided math has many benefits although organizing the groupings can bring a few challenges. Guided math looks different depending on how the teacher implements the structure. For example, one math group might be working with the teacher while two other groups are using math games or participating in problem based learning activities. The groups will rotate according to a specific time schedule. I’m finding that groups that are not with the teacher need specific instructions and expectations.

For the past few months I’ve been using dice games to emphasize number sense skills. These dice games have peaked student interest and work well in increasing computation fluency. I decided to collect multiple formative data pieces to validate whether the dice games were contributing to student success. By analyzing student data and observing over a period of time, I found that students were becoming more fluent in adding, subtracting, and multiplying small/large numbers.

The games have worked for me, so I’m passing it along to others that might find it useful. Needed materials and pdf files are below.

Materials

A variety of dice (6, 10, 20, 30, etc. dice) Here are some examples:

Templates (in pdf form)

Roll to 150 (multiplication)

Roll to 125 (addition)

Roll to 100 (addition)

Roll to 45 (addition)

Roll from 50 (subtraction)

Roll from 95 (subtraction)

Roll from 35 (subtraction)

Student Data and Balance

Teachers in K-12 often use student data on a regular basis. Student achievement data can be used to qualify students for reading, gifted, remedial, enrichment, acceleration, differentiation, and a variety of other services. Recently, standardized testing data has been the forefront of educational trends and in the news. Implementing a balanced approach when looking at student data can keep stakeholders (educators and administrators) grounded in an understanding that the numbers behind the tests may give light to areas of strengths/needs.

Data isn’t evil

Assessing a student’s understanding of a specific concept isn’t necessarily a bad thing. In fact, over the past few years I’ve grown to appreciate and utilize student achievement data more and more. Whether the data is from a standardized test or not, the data can be helpful if used correctly. Moving data beyond just a number can benefit teachers and students. Data can help teachers ask better questions and provide opportunities to reflect on how students learn best. Involving students in analyzing their own data can encourage student goal setting and ownership.

Having conversations with students about their data is powerful.

Have the conversation

I’m definitely not an advocate for having additional standardized tests, although some seem more useful than others. I find that assessments that give detailed feedback (e.g. areas that need strengthening, %ile compared to the norm, strength areas, next instructional steps, etc.) are more frequently used by teachers, compared to assessments the give little feedback. Obviously, there isn’t a perfect test available for school purchase. The assessments that a school uses should give detailed feedback that can be immediately used.

Do you hear a lot of negative talk in regard to standardized assessments? Having a conversation about an assessment’s effectiveness in informing instruction may be needed. Instead of trash talking the assessments in general, educators and administrators should find assessments that work for them. PLC teams should emphasize the importance of using formative assessments regularly. I’ve found that teacher created formative assessments are some of the best ways to find areas that need strengthening and to identify differentiation opportunities. The purpose of giving the assessments should be communicated to all stakeholders. When teachers understand why the tests are given, (not just for VAM reasons), they may start to value the benefits of assessing students using a variety of tools (such as Common Core performance assessments).

Balance is needed

With teaching and in life, balance is needed. Teaching is a profession that can be stressfull. It has many teachers thinking right now, how many days till Spring Break?? Balancing assessments with instruction takes skill and patience. Standardized tests are often at the forefront of school administrator’s minds. One test shouldn’t be used to determine if success, or enough growth has been made to call that school year/class/school successful. Take a breath and look at assessments from a macro lens. A combination of formative, informal, formal, review checkpoints, activators, performance (insert your assessment here), and even standardized assessments have their place in a school and can be beneficial to a certain extent. The value of the data often depends on how it’s utilized.

Picture Credit: DigitalArt

“Your assumptions are your windows on the world. Scrub them off every once in a while, or the light won’t come in.” Isaac Asimov

Web-Based Formative Math Assessments

I’ll admit it, I’m becoming more of a formative assessment advocate this year. I believe that formative assessments have a place in the elementary math classroom. As a technology enthusiast, I’m always searching for ways to improve my instruction through the use of technology. For the past year I’ve had the opportunity to use Socrative and Scootpad apps (both free) with my math class. Both of these apps are web-based and offer the ability to provide immediate feedback to the student. I’ve added a few snippets of information about these apps below.

Socrative is a web-based program that is similar to a wireless clicker system, but with a keyboard. Teachers can create multiple choice, true/false, and short answer quizes with this app. The quizes are quick and easy to create – I actually created a 10 multiple choice question quiz on an iPad. Teacher have the option for students to complete the quizes at their own pace or at an assigned pace as a class. Similar to Google Docs, student information is updated and you can actually show the data on an LCD screen live. Once short answers are submitted students also have the option to vote for the answer they feel is best. This option definitely promotes student engagement. Reports on student progress can be sent to you via email and they are in Excel format for easy sorting.

Scootpad offers teachers a way to assess students on Common Core Math Standards (Grades 1-5). Teachers are able to individualize assessments based on the needs of their students. Mastery (as a %) can be determined by the teacher and students have opportunities to earn badges and other awards. The interface takes a while to get used to, but overall this app allows teachers a quick opportunity to assess students’ understanding. Student data is aggregated and can be sorted easily. Scootpad will be expanding to middle school math Common Core Standards in the near future.

What formative assessments do you use?

The Marshmallow Challenge in the Elementary Classroom

Using Food to Learn — Creating Structures with Collaboration

Approximately two months ago I noticed a Twitter post about something called the Marshmallow Challenge. The tweet led me to this TED video. Many of the examples indicated that the challenge could be used with adults as well as students. The official Marshmallow Challenge website offers many useful instructions and tips for facilitators. I decided to use the challenge with a fourth grade classroom. The session, from start to finish, took approximately 45 minutes. The standard 18 minute time limit to work on the project was perfect for my classroom. Of course the focus of this project emphasizes teamwork, but I decided to add a few measurement standards. For example, the students were required to measure the length of each pasta stick used and find the volume of the marshmallow (as a cylinder). The total height of the structure was also measured. Here are a few pictures from the event:

This slideshow requires JavaScript.

The class had a debriefing session after the event. During this discussion, students revealed their strategy. Here were some of the questions that were discussed.

What will the base of the structure look like?
Will we use all of the materials?
What are our roles?
How will we work as a team?
How does working as a team help us succeed?
Will we wait to put the marshmallow on top at the very end or test it throughout the project?
Should we write out a plan in advance?
How should we work together?
What are other groups doing?

Overall, this learning experience gave students an opportunity to use critical thinking in a collaborative setting. I’m planning on having students complete a plus/delta chart and complete an entry in their math journals next week.

*Picture credit: Stoon

Measurement and Mini Golf

Approximately a week ago I was paging through my math curriculum. Through a pre-assessment I found that students were in need of a review on angle classification and measuring skills. The curriculum lessons offered a number of worksheets and angle measuring drills. Although these lessons seemed beneficial, I felt the need to create a more memorable learning experience for my math students. At this point, I decided to search for measurement projects. While following #mathchat, I came across this Edgalaxy site. The project seemed to match many of the objectives that needed strengthening in my class. I changed up the directions and modified some specifics in order to best meet the needs of my students.

So … a week has passed and almost all of the projects are complete. I listed the project steps below. Feel free to use any of the ideas below in your own classroom.

1. Had out the direction sheet. Here is a Word template (via Google Docs) for your use.

2. Review many of the different vocabulary words associated with the project: acute, obtuse, right, parallel, perpendicular, trapezoid, etc.

3. Show possible examples. I tend to show just a few examples as I don’t want to give them a mini golf course to copy.

4. Group the students into pairs. If you prefer, this project could be implemented as a collaborative group activity.

5. Students choose their construction paper color (11″ x 20″)

6. Students draft their course in pencil (on grid paper). The draft gets approved by the teacher and then is transfered to scale on construction paper.