Last week my second grade crew explored fraction blocks. They cut out and used the blocks to compare fractional pieces. Students enjoyed the trial-and-error component and they started to visualize fractions in a different way.
I decided to use a similar activity with my third graders. Instead of labeling the bars, I decided to leave off the label. This initially confused the students as they expected to see the label. Students moved beyond the confusion when they were given the value of one of the blocks. They then used that value to compare all the other blocks. Students were asked to cut out the blocks and start comparing them. I didn’t give them any directions beyond that. After about 4-5 minutes I placed the sheet below on the overhead projector.

We completed the sheet as a class. I used the document camera and students compared the pieces on their own desk. It took multiple attempts and a number line, but eventually the class was able to finish the sheet. Students were then off on their own to find the whole or part of certain blocks. Students used many different strategies since they couldn’t rely on the label. 
While the students were working I went to the different tables and observed the strategies. Almost all the students compared the shapes to one another to find one whole. Other students created a number line and placed where they thought each shape would be located. I had a few students take out a ruler and measure the blocks.

I collected the sheets once everyone was finished, marked them up with feedback, and returned them the next day. I used the NY/M model for this assignment. Every student in the class needed to make some type of correction. After a brief review, I gave the students back their sheets and they made corrections. There were few perfect scores after the second attempt, but everyone improved – an #eduwin in my book.
Download the file for this activity here.
Next week we’ll be learning about equivalent fractions and how to find common denominators.

















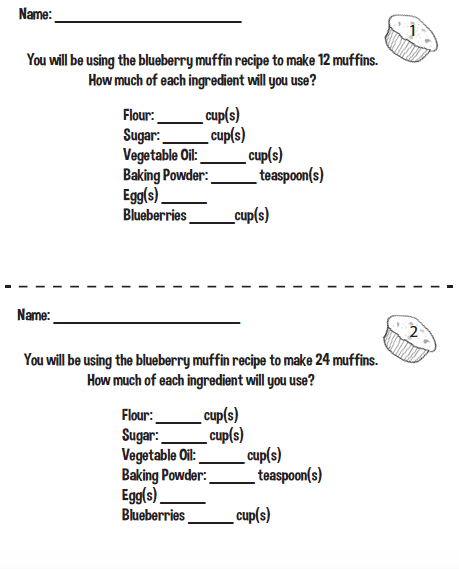
 Similar to last year, students had to change the recipe based on the amount of muffins needed. Unlike last year, I didn’t introduce the fraction multiplication or division algorithm. I had students work in groups and document their strategy to find a solution.
Similar to last year, students had to change the recipe based on the amount of muffins needed. Unlike last year, I didn’t introduce the fraction multiplication or division algorithm. I had students work in groups and document their strategy to find a solution.