Coordinate Grids – Part Two

Screen Shot 2016-01-16 at 11.04.49 AM

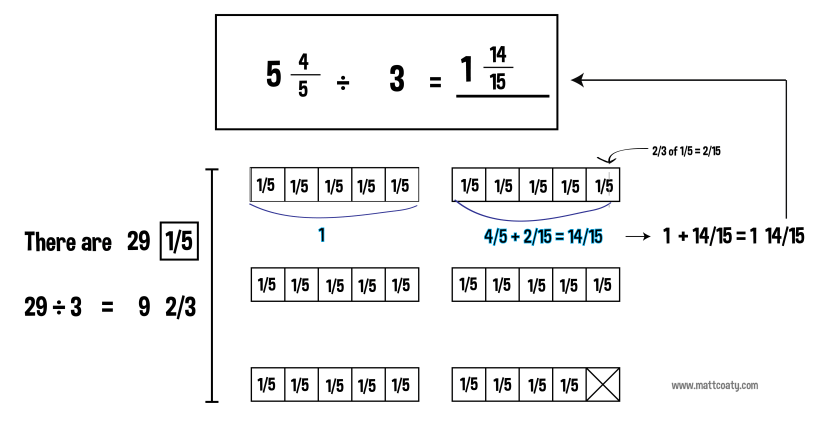
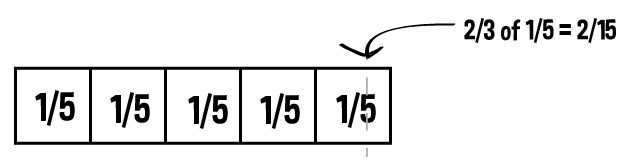
Last week my students started to plot points on coordinate grids.  They were identifying different quadrants and becoming more confident with drawing shapes on the plane. While reflecting on last week’s activities I noticed a Tweet that was sent our replying to one of my blog posts.

I’m a rookie when it comes to Desmos.  Most of the stories I hear involve middle or high school students. I needed to find something that worked with my elementary kids.  So I started to research and did a little bit of exploring to see how this could be used with my third grade class.  I ended up looking up some of the templates but had a bit of trouble finding an extremely basic rookie-like coordinate plane activity for my students.  I decided to go the route of creating a template and having  students manipulate created points for a project.  Click here for the template.

I quickly found that students had no idea how to use Desmos.  I gave the students 5-10 minutes to orient themselves.  Students were asked to move the points to certain coordinates  on the grid.  As they moved the points students started noticing that the tables on the left side of the screen changed.  Students started connecting how the tables changed and this helped reinforce concepts learned last week.  After this introduction time, students were given a rubric that contained the following:

  • Move the points on the grid to create two angles
  • The angles need be located in two different quadrants
  • The angles need to be acute and obtuse with arcs located in each one
  • Indicate the measurement of each angle

Students were then given 15-20 minutes to create their projects.

Screen Shot 2016-01-16 at 10.37.39 AM

Students created their angles by moving the points around the grid.  Students then shared their projects with the class.

Screen Shot 2016-01-16 at 10.44.32 AM

Students took a screenshot and then added the degree measurements to the angles.  The class reviewed the projects and students explained how they plotted the points.  This project seemed to help students make the connection between points and the x and y-coordinates.  It also reinforced skills related to angle classification and measurements.  I’m looking forward to expanding on this project next week.

Exploring Coordinate Grids

Photo Jan 07, 9 16 05 AM

My third graders started to explore coordinate grids this week. For many, this was the first time that they’ve used them. Some of the students have played Battleship or some other game that involves a grids.  Playing off that background knowledge, I used a road map to show how people can find certain locations by using a coordinate grid. This made sense to some of the students but a few still were unsure of what axis was used first to determine where to plot a point.  This was a reoccurring theme throughout the lesson.

During this process I remembered a strategy that another colleague suggested a few years ago. She borrowed the idea from another teacher and it seemed to work well in her classroom. A colleague of mine used (3,2) as an example of the “go into the building” – first number (right 3) and then “go up or down the elevator” (up 2) method. I decided to use that strategy and a few more students started to grasp the process.  The next activity in the paragraphs below seemed to solidify a better understanding for the rest of the class.

Earlier in the day I created a very short Nearpod lesson involving mostly pictures of coordinate grids. I handed out a iPad to each student. Students logged in and given a picture of a grid and asked to draw and label points.

nwBSug

I then revealed the pictures to the class on the whiteboard. The names of the students were hidden so that we could analyze each response without throwing judgement lightning bolts towards a specific individual. As the class went through each picture they started to notice trends.

Photo Jan 07, 9 20 58 AM

  • Some were switching up the x and y-axis numbers
  • Some were not creating a point
  • Some were not creating a letter for the point
  • Some were confused by the negative sign in front of the numbers

Students observed these issues from the first question and grid. After a decent discussion on the above trends, the class moved towards the second grid and question. I gave the students that same amount of time and the results seemed to initially improve.

Photo Jan 07, 9 26 56 AM

Students started to become better at finding their own mistakes before submitting their creations. I used the same strategy as earlier and displayed the results to the class. There were a few that had some of the same misconceptions, but not as many. In fact, many students vocalized the class improvement since the last question. One of the evident misconceptions revolved around students having trouble plotting negative numbers on the coordinate grid. The class discussed this and completed the third question and grid. The student responses from this question were much better than the prior two. Students were starting to develop some true confidence in being able to correctly plot points on a coordinate grid. I kept a list of the trends that students noticed and will bring it out later in the unit as we’ll be revisiting coordinate grids next week.

Photo Jan 07, 9 25 57 AM

After our Nearpod lesson (which was about 15-20 minutes) students played a Kahoot on identifying points on a coordinate grid. I felt like this was helpful as students identified the points and were able to gauge their own understanding compared to the goal.

Minecraft and Math

Photo Dec 16, 9 08 35 AM

Earlier in the school year a group of three teachers at my school wrote a grant expressing the need to incorporate Minecraft in the classroom. The idea actually started last summer when a colleague and I attended a professional development event in Downers Grove. During one of the sessions I met two teachers from nearby school districts that used MinecraftEdu in a school club. What they had to say caught my interest and two other teachers and I decided to start a school club in 2016. We wrote the grant and it was accepted. Last week the licenses were purchased and I’ve explored the potential of using the program in the classroom setting.

Before the school year started I knew very little about how to use Minecraft. I decided to purchase a copy and explore the Minecraft world over the summer. I quickly learned the controls and watched a number of YouTube videos to become a better rookie. I’m still a rookie. I found the MinecraftEdu community online and started posting questions to the forums. Moderators answered my questions and I started feeling more comfortable using the program on my own. The forum has been especially valuable in giving me ideas to use in the classroom.

I downloaded a few world templates and started brainstorming. I then bounced a few ideas off of colleagues and decided to start using the program for a math scavenger hunt. The goal was to have students get used to using the program in an education setting while reviewing fraction math concepts in the process.  Most students already understood the controls and the game but weren’t used to using it for a different purpose.  I wanted to start simple and I thought a scavenger hunt would be an easy way to start incorporating the program in my math class.

Math scavenger hunt – third grade

Photo Dec 16, 9 08 01 AM

Students entered into the fraction world that I created.  Once they entered into the world I froze all of them. I explained the goal of the world and answered questions. The goal was to explore the world and find the signs that were posted. Students were using the MinecraftEdu version where they weren’t able to build or keep inventory of items. Trap doors, caverns and bridges were all part of this simple world. Each sign had a particular math problem on it and students were expected to solve the problem. I then passed out a sheet that went with the scavenger hunt. The sheet had spaces for students’ number models and solutions.

I then unfroze the students and they were off to the races. Students split up and started exploring the area. They soon found that working in teams seemed to be more efficient in finding the signs. All students were finished with the scavenger hunt in 30 minutes. Afterwards the class reviewed the answers.

House building – fifth grade

gfqcpr

I created a completely flat Minecraft world for this activity. Students were grouped into teams and given a task related to concepts that we’ve been discussing. The fifth grade class has explored area and perimeter and will eventually be investigating volume in January. Each group was asked to create a building that met a certain criteria. It was stated that each Minecraft “block” was exactly 2 feet on each side. Those measurements were used to meet the criteria.

Screen Shot 2015-12-20 at 9.09.26 AM

Students worked together and started building their houses. A few groups had to restart as they found out that the perimeter and area didn’t meet the criteria. After around 30 minutes students are about 50% complete with their houses.  I’m assuming that another 30-40 minutes and the students will be finished with their projects.  At some point after break the class will be presenting their buildings to the class.

In January my school will be offering a Minecraft club to around 25 elementary students. We’re planning on building our actual school from scratch using some type of scale model. The students are already excited to be using this program in school and I’m looking forward to what students create and the process involved in that creation.

Math Intervention for Enrichment

Screen Shot 2015-12-13 at 11.52.36 AM.png

This school year I’ve been given the opportunity to work with a select group of second grade math students.  Since early October I’ve been seeing two groups of around 20 students for approximately 30 minutes twice a week.  These 40 students were selected based on unit pre-assessment scores and teacher recommendations.  The second grade students that I see tend to be in need of enrichment of the math skills that they’re exploring in class.  This enrichment can take on many forms, but mainly I’ve been looking at have students develop a better understanding of numbers and patterns.  I’ve been asked to expand on the unit being taught in class and report back progress that students have been making.  The groups that I see are designed to be flexible and change depending on a particular math unit.

 

Here area  few things I’ve observed as the year has unfolded:

1.)  30 minutes twice a week is a short time period.  I’m all for packing in as much instruction as possible, but 30 minutes goes by very quickly.  I’ve had to redesign many of my lessons to overlap the two days in a week.  Retention can also be an issue with this.  I spend each session with a bit of review and that has seemed to help.

2.)  I’ve had to incorporate my own pre/post-assessment to show student growth.  At first I thought this was extremely time consuming as students only have a small amount of time in my class and I want to make sure that the class time is being used appropriately.  This year many of the classes in my school are using the same pre-test as the post-assessment.  I’m using that model right now but it may change as the year progresses.

3.)  I’m not able to meet with the second grade team every week so we decided to use Google Docs as a communication tool.  My students’ pre/post assessment scores are located in the shared doc and can be assessed by any of the second grade teachers.  I also attached a copy of the pre/post assessment to the document so teachers are aware of what topics I’m addressing.

Screen Shot 2015-12-13 at 11.43.30 AM

4.)  I’ve been using effect size to show student growth.  I learned about effect size in more detail after attending a Visible Learning conference over the summer.  I feel like this has been a useful tool and has shown some insight into student gains in my class.  This tool has also been important as it brings some finality to the units that I teach and can be used as one data point in transitioning students in/out of my class.

Screen Shot 2015-12-13 at 11.44.03 AM.png

5.)  Student reflection is key.  This year I’ve been giving students a copy of their pre-assessment stapled to their post-assessment.  Students are then able to review their growth and ask questions.  The focus is on student growth and not necessarily on point value or grade.  Thankfully at second grade students aren’t used to traditional grades yet.

 

I’m looking forward to seeing how this enrichment opportunity develops over time and the positive impact it has on students.

 

The Power of Visual Models

Anchorchart

My fifth graders started off the week learning more about fractions.  On Monday students used a visual model to multiply mixed numbers.  The visual model was a bit challenging for students to grasp.  Many of the students knew parts of a multiplication algorithm, but not necessarily how to show the computation visually.

muliplyingfractions-01

It took a decent amount of modeling and experimenting, but I believe completing the visual models increased students’ understanding of fraction computation.  After a decent dose of the visual model, students were introduced to a fraction multiplication algorithm.  I tried to make the connections between the algorithm and visual model as apparent as possible.  Many students made the connections, but not all.

Around mid-week students started to divide fractions.  Again, I started off the discussion around using a visual model to show the division.

fraction division-01

This time students were more confident in creating the visual models, although some wanted to jump to the standard algorithm.  This stopped once I included the visual model as part of the steps required to solve the problem.  Some of the students that had trouble creating the visual model for fraction multiplication started to become more comfortable with the division model.  This was good news.  The most challenging part for my students was finding a fraction of fractional pieces.

Screen Shot 2015-12-05 at 8.54.53 PM

This was solved once students realized that “of” meant to multiply and then they were able to find a solution. The class had many light-bulb moments as students made connections between the visual model and standard algorithm.   Also, one of the additional benefits was observing students look at the reasonableness of their answers.  This was more apparent when students created a visual model first.  The class will be sharing their models next week.

 

Screen Shot 2015-12-05 at 9.08.31 PM.png

 

I’m finding that there’s power in using visual models.  The opportunity to use trial-and-error with visual models has many benefits.   It’s a low-risk opportunity that allows for multiple entry points.  Students are making sense of fractions before moving to the standard algorithm.  It might not be the most efficient way to compute fractions (as students continue to find out), but I believe students will have a better understanding when they can visualize fractional pieces and then use a process to find the solution.  At some point students will be shown a visual model and be asked for the computation.  I feel as though students were steadily building  their conceptual understanding  of fractions this week.

Roller Coasters and Math

Screen Shot 2015-11-29 at 7.55.48 AM

One goal this year is to have my classes complete more interdiciplinary projects. These projects move beyond district-adopted texts and often involve multiple subjects and student groups.  I find value in having these projects as students often need to work in teams and apply their mathematical thinking in different situations.

Back in September I came across the tag #paperrollercoaster.  After completing a quick search I came across multiple pages where teachers had students create paper roller coasters and answer questions.  The questions were often related to math/Science objectives.  I thought this had potential so I finalized a decision and ordered a set from here.  My thinking was that if one worked out well I might order more.

Screen Shot 2015-11-29 at 8.30.29 AM

The materials arrive around a week after I placed the order.  I decided to use the project with a third grade class.  After a brief explanation, students were placed in three groups.

rollercoaster-01

One group drew out and created an outline for the base on a piece of cardboard.  The group was asked to create six square bases where students would be placing support columns. The second group scored, cut out and attached the base columns together to be placed on the outline of the first group.  The third group was in charge of creating the support beams. Students scored, cut out and opened up both ends of the beams so they could be added to the columns.

All groups had approximately 20 minute to work in their group.  They were supplied with tape, scissors and directions.  Afterwards, the class met in the front of the room and we started to build the base for the roller coaster.  During that time the class started to discuss some of the math vocabulary we’ll be using as the building continues. Most of the terms will be coming from the geometry and measurement math strands.  The terms area, surface area, volume, length, formulas, speed and height were all discussed before the students left for their next class.  I appreciate the multiple math entry points available through the use of this project.  As the project progresses I’m planning to add activities/sheets that we use.  In the meantime, feel free to check out a few lessons here.

 

Multi-digit Multiplication Strategies

 

Multiplication strategies-01

This past week my third grade class investigated different ways to multiply numbers.  Before diving into this concept I asked the students their thoughts on multiplication.  A few students explained to the class their view on the topic of multiplication.

  • repeated addition
  • double or triple “hopping”
  • using arrays
  • “timesing”
  • Increase the number by “a lot”

Most students were able to showcase examples of the above.  Even though their vocabulary wasn’t exactly spot-on, students were able to come to the whiteboard and show their thinking.

I received different responses from the students when asking them about multi-digit multiplication.  Actually, it was more of a lack of response.  I feel like some of this is due to exposure.  A few students raised their hands and asked to show their process to multiply multi-digit numbers. These students showcased their ability to use the traditional algorithm. The class reviewed this method with a few examples.  Although students were finding the correct product they had trouble explaining the process. Students weren’t able to communicate why it worked or another method to find a solution.

On Tuesday my class started to explore the partial-products algorithm.  Students were able to decompose individual products and find the sum.  This made sense to students.  Students were able to connect an area model with the partial-products method.  They started to write number models right next to each partial-product.

Later in the week students were introduced to the lattice method.  This method seemed “fun” for the students, but didn’t make as much sense as the partial-products method.  Students were able draw the boxes and create diagonals to find the product.  Some students had trouble with laying the boxes out before multiplying.

During the last day of the week students were asked to explain in written form how to multiply multi-digit numbers.  Even though all of the students could use the traditional, partial-products and lattice methods, they were stuck for a bit.  Soon, most students started to lean towards using the partial-products method to explain how and why this method works.  I asked one student in particular why it made sense and she said “I can see it visually and in number form.”  Although most students were able to use the other methods effectively they didn’t seem confident enough to explain why the strategies worked.

Students will be expected to multiply multi-digit numbers on the next unit assessment.  The method to multiply these numbers will be determined by the student, but I’m wondering how many will gravitate towards the strategy (not just the process) that they understand.

 

 

Mindframes and Teaching

Screen Shot 2015-11-07 at 9.27.27 PM

This last Thursday I was fortunate enough to attend a conference around the topic of visible learning in schools. The conference had so much information.  I had to filter and compartmentalize the discussions and presentation.  One of the discussions revolved around John Hattie’s effect size and how schools can make learning visible in classrooms. The last day was dedicated to organizing a school plan that’ll be carried out through the remainder of the school year.

One of the more memorable pieces of the conference were the discussions that happened between the school teams.  My school sent a team of four teachers and two administrators to this particular conference. Discussing our views on teaching and learning was a powerful experience. Many members of the team don’t regularly work with one another, so meeting to discuss these issues brought about other views as we’re all in different roles . Not everyone thinks the same and each member of the team was willing to hear out different perspectives. As a team, we agreed that our school has some great initiatives happening right now. That affirmation was great to hear, but at the same time, we felt that there are steps we need to make to become better. In order to put these initiatives in place the school has to communicate the importance and reasoning behind these proposed changes.

This brought up another discussion about how change will not happen unless stakeholders are truly committed to the cause. Even if they’re committed, the initiative doesn’t reach its full potential unless the organization and individuals have mindsets that are aligned with the initiative. This type of thinking falls in line with Hattie’s Mindframes for Teaching. Teachers have beliefs that impact their teaching. That belief often stems from a self-developed mindframe. Understanding your own mindframe can help stakeholders better define their own role.  The mindframes are explained in the video below.

All of these mindframes are discussed in Hattie’s Visible Learning book.

Early in September my school was introduced to the idea of teacher mindframes. A staff meeting was designed to have educators analyze Hattie’s mindframes and reflect on their own. We plan on revisiting this topic throughout the school year. Understanding deep-seeded beliefs about our role in education can help bring awareness to how we think.  I believe that thinking impacts instructional decisions that influence student learning.

Exploring Criteria for Success

criteria-01

This past week I’ve been observing how students reflect on their learning. This observation originated from a brief conversation that I had with an administrator about the need for students to be aware of the mastery learning objective. Depending on the lesson, I feel like being aware of the goal upfront is important as students have an understanding of what’s expected. Although posting an objective brings awareness and is easy to check-off during a class walkthrough, it doesn’t necessarily impact student learning.  At the most, posting the objective may direct students to informally question the connections that they’re making in relation to the goal. To ensure that students are making a personal connection to the goal I believe they need to have ample opportunities to reflect on progress made towards the goal.

mlo-01

That reflection process becomes important as students start to recognize their own growth over time. This year I’ve been giving students time to review assessment results and compare their results to specific math standards. In the past students have used math journals and a reflection sheet to document their progress. At this time of the year students are using it every 2-3 weeks and it’s a bit sporadic. I’m trying to become more consistent with giving students time to compare their academic progress to the expected goal. In general, I want students to become more capable of self-assessing their own progress. I believe moving towards a criteria for success model may help.

criteriapicI first heard of criteria for success during a Skillful Teacher class that I took awhile back.  This past year I’ve been experimenting with using it more frequently.  I’ve been finding that the criteria for success communicates what meeting the standard looks like. It also tells students if the product that they created is good enough to meet the standard. I think of it has an expectation gauge. If students can recognize that they’ve met the criteria for success then they’re meeting the minimum expectation for that particular assignment. Josh Hattie has been quoted as saying a visual learning school is “when kids know what success looks like before they start.” See Hattie’s video here for a more in-depth dialogue on his view on criteria for success. My first thought of criteria for success revolves around the idea of rubrics. But it doesn’t end there. A decent rubric can tell students if they’ve produced work that has met the standard. Personally, I feel like a rubric can’t be used for all assignments and projects. A criteria for success can also take the form of a checklist or list that describes the qualities of a proficient project.

question-01

Should the criteria for success be used for every lesson? Right now I’m tackling this question. I’m wrestling with it because students complete so many activities and assignments that narrowing it down to just one a seems unmanageable. Also, sometimes students work on projects that last a couple of days. In those cases, does the criteria for success stay the same and do students periodically revisit it accordingly?

I’ve been using criteria for success checklists over the past few days and am analyzing the results. I’m finding that students are intentionally reflecting on whether they’re meeting the posted objectives. Students that analyze their own performance have opportunities to also set goals and move forward. I see potential in using this model as students become aware of their own performance level compared to the standard.

journalentry